Just why are fractions so confusing?
What happens after you have coloured squares and cut and stuck endless circles, cut cakes, made pizzas, folded paper strips, made fraction walls, chanted rhymes . . . and they don't get it? Here are some clues and insights into the common misconceptions about fractions.
Fractions are introduced from the early years in school, yet it remains a difficult concept to secure. This is one of the most challenging aspects of fractions - to understand that ¾ is one number and using fraction number lines helps establish this concept. Annotation and visual representation are effective strategies in working with fractions. Reinforcement of the meaning of the denominator helps establish division or the breaking of a number. It is also helpful to introduce the Latin root word 'frac' meaning to break and create comic / posters.
It can take a lot of exploration to secure understanding of the part/whole relationship in fractions. After years of mastering the four rules of number (+, -, x /) learners with weak understanding of fractions will default to using the operations they understand and will frequently +, x the numerator and denominator when working with fractions. This gives strong diagnostic evidence of misunderstanding of the concept.
“What appears to be critical in learning is that the use of physical tools leads to the use of mental models, which builds students’ understanding of fractions (Cramer & Whitney, 2010; Petit, Laird, & Marsden, 2010). ”
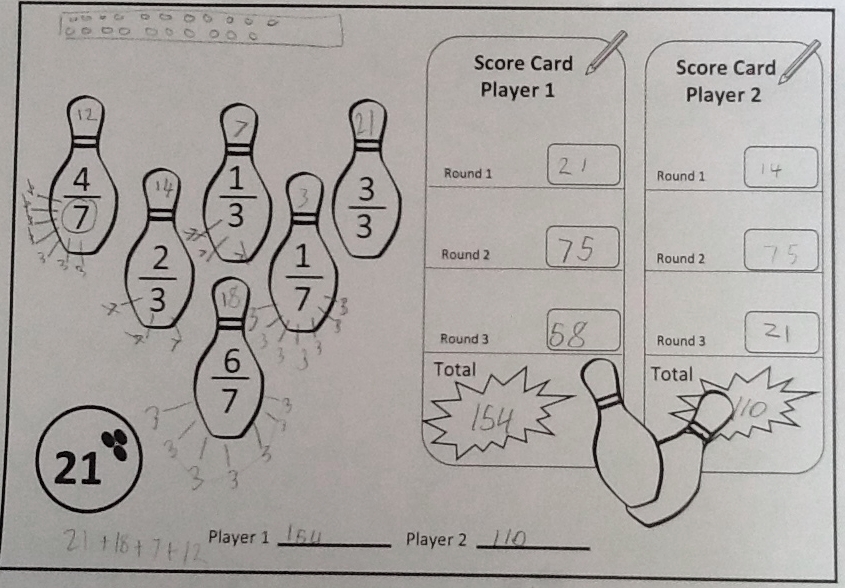
Here are some games that are highly motivating and the learner practically forgets they are learning - giving many opportunities for over-learning and establishing a concrete understanding of the constructs of fractions.
For a dyslexic learner the use of visual mapping is critical to developing concepts. The adage of 'multiply the top and the bottom by the same number' makes little sense and the overload on working memory makes the strategy less accessible. Exploration of fractions by modelling using diagrams and a wide range of manipulatives allows the learner to build experiential knowledge with concrete understanding of the relationship between the denominator and the numerator. Equivalent fractions are ways of describing the same amount by using different-sized fractional parts.
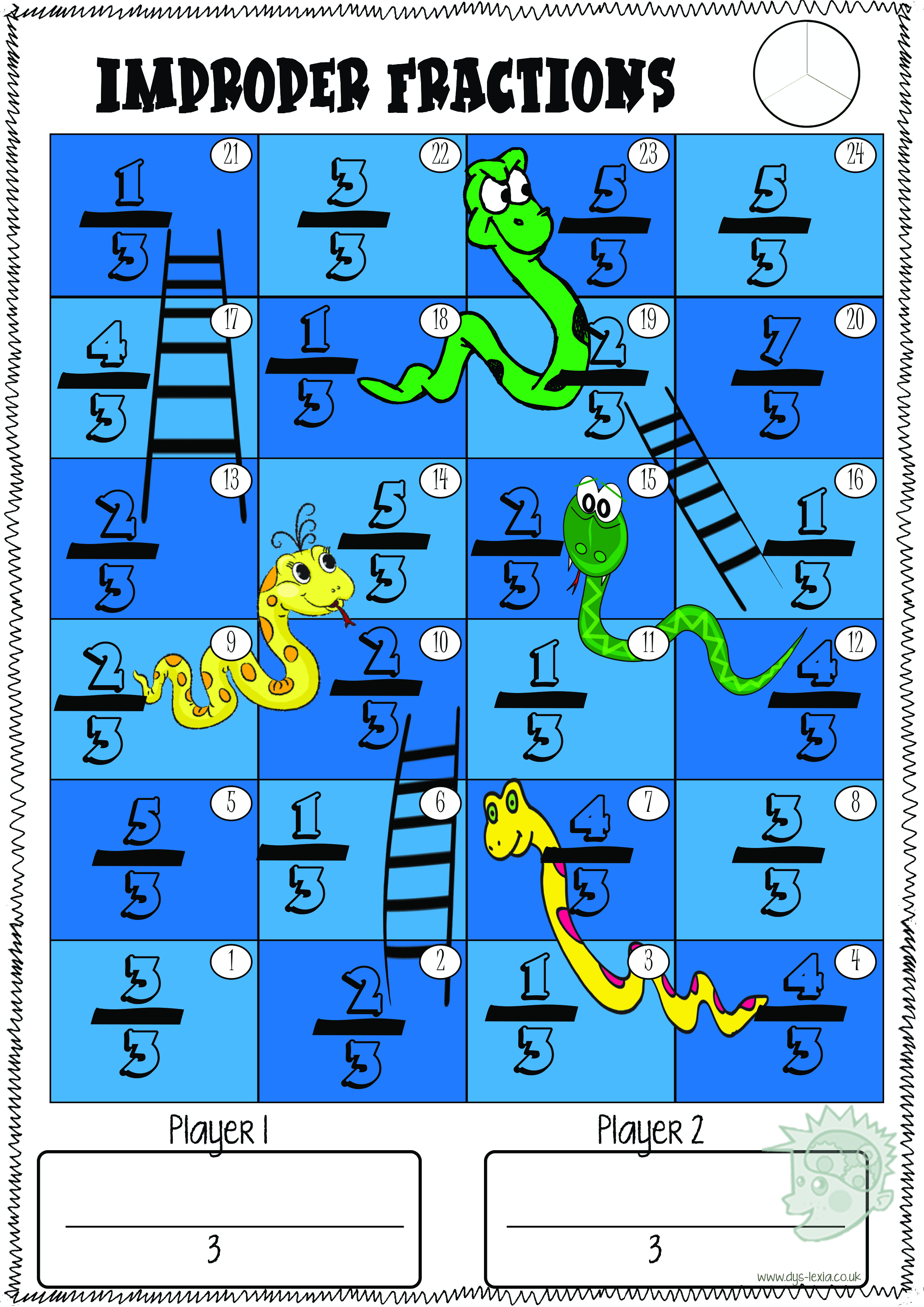
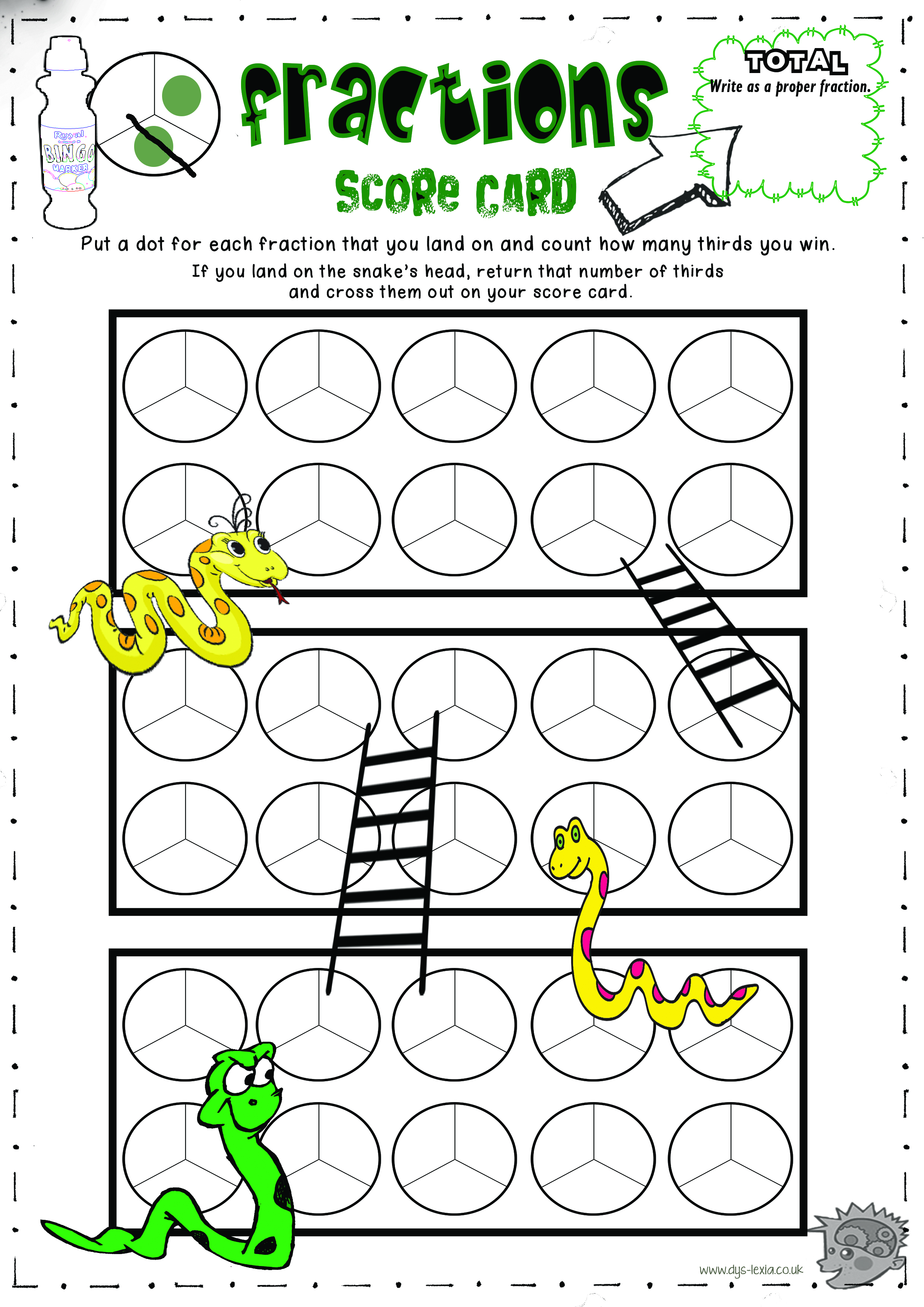
Click here to download the games of snakes and ladders for improper fractions..
Establishing a mental framework of the comparable size of fractions is problematic when the learner does not understand that a fraction is a number, leading them to consider a tenth to be bigger than a fifth because 5 is less than 10. Generalising that the bigger the denominator the smaller the fraction leads to further confusion, for example thinking, 1/5 is more than 7/10.
Another area of difficulty is understanding that 2/3 means two equal-sized parts while not necessarily equal-shaped objects. Creating their own representations of fractions with lots of manipulatives and on paper helps establish this link. Lots of 'teasers' such as playing 'Would you rather. . . have 1/10 or 3/5 of playtime or fewer spellings for homework?' It is also helpful to do the same activity with two different representations and ask learners to make connections between them. For example, if asked who walked the furthest, a linear model is more likely to support their thinking than an area model.
Finally, understanding fractions means understanding all the possible concepts that fractions can represent; part/whole, measurement, division, operator, ratio.
Feel free to get in touch with any questions or to share ideas.